INDEX 
III. Représentation graphique des contraintes
Parmi les solutions possibles d’un problème, il y a ceux qui vont satisfaire toutes les contraintes du programme, appelés solutions réalisables, et ceux qui vont satisfaire une partie ou aucune de ces contraintes, appelés solutions non réalisables.
Une représentation graphique des inégalités (des contraintes) va nous permettre de déterminer l’ensemble des solutions réalisables.
Revenons à l’exemple 2 du problème de médecine.
Une des contraintes de ce problème est celle relative au grain d’aspirine :
.
L’ensemble des solutions qui vérifient cette inégalité est le même que celui qui vérifie 
et 
.
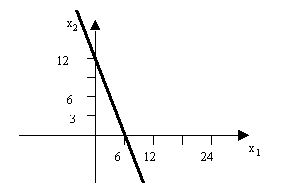
L’ensemble des solutions qui correspond à l’équation est l’ensemble des points de la droite l définie par 
. Cette droite admet une valeur de la pente égale à –2 et intercepte l’axe des ordonnées en 12 (voir figure ci-dessus).
L’inégalité correspond à un demi-plan limité par la droite . Or cette droite divise le plan en deux demi-plans ouverts donc quel est le demi-plan à choisir ?
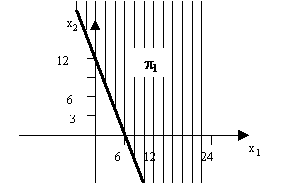
Pour ce faire, il suffit de prendre un point de l’un des demi-plans (c’est à dire n’appartenant pas à la droite ) et voir s’il vérifie l’inégalité . Par exemple le point de coordonnées (0,0) ne vérifie pas l’inégalité donc le demi-plan
L’espace hachuré représente le demi-plan fermé des solutions qui vérifient la contrainte .
Si on fait de même pour les deux autres contraintes du problème (voir figures
ci-dessous), on obtient les deux autres demi-plans
et 
.
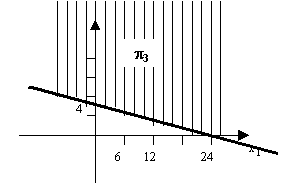
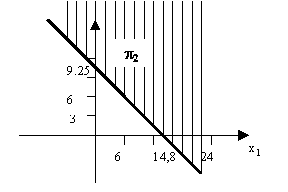
Une solution possible du problème est dite réalisable si et seulement si elle vérifie toutes les contraintes, c’est à dire si elle appartient aux trois demi-plans relatifs à chaque contrainte du programme linéaire, en d’autre terme à
p 1 Ç p 2 Ç p 3 (voir figure).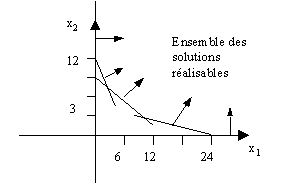
Définition :
Un ensemble E non vide est dit convexe si et seulement si pour tout élément x et y de E et pour tout l Î [0,1], l x + (1-l ) yÎ E.On peut vérifier facilement que chacun des demi-plans
p 1, p 2 , p 3 est convexe en vérifiant que pour toute paire de points P1 et P2, l’ensemble des points qui forment le segment [P1P2] appartient au demi-plan.Théorème :
L’intersection d’ensembles convexes (non vide) est convexe.Propositions
: L’ensemble des solutions réalisables (non vide) est convexe.
Cliquer ici pour enregistrer le chapitre 2 en format Word sur votre disque dur (452 Ko)
Pour tout commentaire envoyer un mail à hatem_masri@yahoo.com