INDEX 
Exemple 5 : Problème de mélange
Un industriel veut produire un alliage Z à 30% de plomb, 30% de zinc et 40% d’étain. Supposons qu’il puisse se procurer sur le marché des alliages A, B, C, D, E, F, G, H, I dont les compositions et les prix respectifs sont donnés dans le tableau suivant :
|
Compositions des alliages |
A |
B |
C |
D |
E |
F |
G |
H |
I |
Alliage à fabriquer |
|
Plomb |
10 |
10 |
40 |
60 |
30 |
30 |
30 |
50 |
20 |
30 |
|
Zinc |
10 |
30 |
50 |
30 |
30 |
40 |
20 |
40 |
30 |
30 |
|
Etain |
80 |
60 |
10 |
10 |
40 |
30 |
50 |
10 |
50 |
40 |
|
Coût au Kilo |
4.1 |
4.3 |
5.8 |
6 |
7.6 |
7.5 |
7.3 |
6.9 |
7.3 |
|
Combien doit-il acheter de chaque alliages A, B, C, D, E, F, G, H et I pour obtenir au prix de revient minimum un 1 Kg de l’alliage Z ?
Formulation en un PL :
La décision à prendre : Combien acheter de chaque alliage A, B, …, I ?
Les variables de décision sont :
On vérifie bien que les variables de décision xi , i= A, B, …, I, sont positives : 
.
Les contraintes relatives au problème sont :
La fonction objectif dans cet exemple représente le coût d’achat des différents alliages A, B, C, D, E, F, G, H et I. Donc l’expression de la fonction objectif est la suivante :
Le programme linéaire qui modélise ce problème mélange s'écrit :
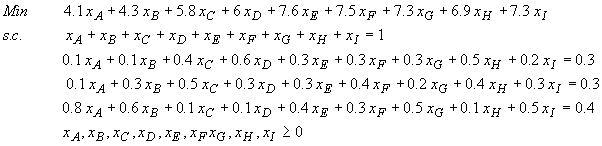
Cliquer ici pour enregistrer le chapitre 1 en format Word sur votre disque dur (172 Ko)
Pour tout commentaire envoyer un mail à hatem_masri@yahoo.com