INDEX

b. Problème du type plus court chemin

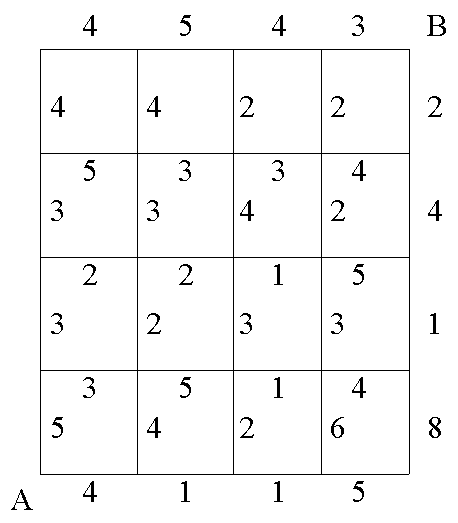
Quel est le plus court chemin de A à B ?

Solution:

On considère l'ensemble des états les point d'intersection sur les diagonales. Ainsi on a exactement 8 étapes.

fn(S, xn) = Csxn + fn+1 (xn), n=1,...., 8

avec f*n+1 (s) = fn(S, xn) et f9 (S) = 0

Etape 8

 

f8(S, B)

 

 

x8 S

B

(S)

1

3

3

B

2

2

2

B

 

Etape 7

 

f7(S, x7) = Csx7+ f8( x7)

 

 

x7
S

1

2

(s)

1

7

-

7

1

2

5

6

5

1

3

-

6

6

2

 

Etape 6

 

f6(S, x6) = Csx6+ f7( x7)

 

 

x6

S

1

2

3

(s)

1

12

-

-

12

1

2

9

8

-

8

2

3

-

7

11

7

2

4

-

-

7

7

3

Etape 5

 

f5(s, x5) = Csx5+ (x6)

 

 

x5

S

1

2

3

4

(s)

1

16

-

-

-

16

1

2

16

11

-

-

11

2

3

-

12

8

-

8

3

4

-

-

10

11

10

3

5

-

-

-

15

15

4

Etape 4

 

f4(s, x4) = Csx4+ (x4)

 

 

x4

S

1

2

3

4

5

(s)

1

20

16

-

-

-

16

2

2

-

14

10

-

-

10

3

3

-

-

11

11

-

11

3,4

4

-

-

-

16

20

16

4

Etape 3

 

f3(s, x3) = Csx3+ (x3)

 

 

x3

S

1

2

3

4

(s)

1

12

12

-

-

12

2

2

-

12

16

-

12

2

3

-

-

13

17

13

3

Etape 2

 

f2(s, x2) = Csx2+ (x3)

 

 

x2

S

1

2

3

(s)

1

15

15

-

15

1,2

2

2

16

14

14

3

Etape 1

 

f1(s, x1) = Csx1+ (x1)

 

 

x1

S

1

2

(s)

A

20

18

18

2

 

On peut résumer les résultats de la façon suivante:

Etapes

1

2

3

4

5

6

7

8

9

Chemin optimal 1

A

2

3

3

3

3

2

1

B

Chemin optimal 2

A

2

3

3

4

3

2

1

B

La longueur du chemin optimal (1 ou 2) est égale à 18.

Cliquer ici pour enregistrer le chapitre 7 en format Word sur votre disque dur (436 Ko)

Pour tout commentaire envoyer un mail à hatem_masri@yahoo.com