III. Analyse de sensibilité
Définition
: Une solution de base optimale est dite stable si l’ensemble des variables de base à l’optimum ne changent pas, même si les valeurs de ces variables de base sont modifiées.Dans cette section on examinera la stabilité de la solution optimale d’un programme linéaire suite à la variation de l’un des paramètres de ce programme.
On utilisera pour présenter l’analyse de sensibilité sur ces différents paramètres du programme linéaire l’exemple de l’agriculteur.
Max 100x1 + 200x2
S.c x1 + x2 £ 150
4x1 + 2x2 £ 440
- x1 + 4x2 £ 480
x1 £ 90
x1 ³ 0 , x2 ³ 0
a. Analyse de sensibilité sur les Cj
On cherche à déterminer un intervalle dans lequel peut varier Cj sans que la solution optimale ne change.
Considérons une variation du coefficient Cj de 100 à 100 +
DEn remplaçant dans le tableau optimal 100 par 100 +
D , on obtient le tableau suivant :
|
|
|
|
100+ D |
200 |
0 |
0 |
0 |
0 |
|
|
|
|
x1 |
x2 |
S1 |
S2 |
S3 |
S4 |
|
100+ D |
x1 |
40 |
1 |
0 |
4/3 |
0 |
-1/3 |
0 |
|
0 |
S2 |
60 |
0 |
0 |
-14/3 |
1 |
2/3 |
0 |
|
200 |
x2 |
110 |
0 |
1 |
-1/3 |
0 |
1/3 |
0 |
|
0 |
S4 |
50 |
0 |
0 |
-4/3 |
0 |
1/3 |
1 |
|
|
|
|
100+ D |
200 |
(200+4 D )/3 |
0 |
(100- D )/3 |
0 |
|
|
|
|
0 |
0 |
-(200+4 D )/3 |
0 |
D -100/3 |
0 |
La solution donnée par le tableau reste optimale si
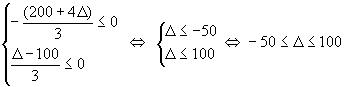
Donc la solution optimale est stable et prend la même valeur (x1,x2)=(40,110) tant que
50
£ C1 £ 200Exercice : Supposons que le coefficient Cj d'une variable hors base dans la solution optimale, est modifié. Dans quel intervalle, Cj peut-il varier sans que la base optimale soit modifiée ?
(Aide : différencier le cas d’un programme de maximisation et le cas d’un programme de minimisation).
Solution :
-
¥ < Cj £ zj cas d’un programme de maximisationzj
£ Cj < - ¥ cas d’un programme de minimisationb. Analyse de sensibilité sur les bj
Déterminer l’intervalle pour lequel, la solution optimale reste stable, pour une variation du second membre de la ième contrainte bi .
Considérons une variation de b1 de 150 à 150 +
D .Sachant que dans le premier tableau de simplexe b1 n’est présent que dans la première contrainte. On obtient ainsi une correspondance entre la colonne des quantités Qi et la colonne de S1.
|
|
|
|
100 |
200 |
0 |
0 |
0 |
0 |
|
|
|
|
x1 |
x2 |
S1 |
S2 |
S3 |
S4 |
|
0 |
S1 |
150+1 ´ D |
1 |
1 |
1 |
0 |
0 |
0 |
|
0 |
S2 |
440+0 ´ D |
4 |
2 |
0 |
1 |
0 |
0 |
|
0 |
S2 |
480+0 ´ D |
1 |
4 |
0 |
0 |
1 |
0 |
|
0 |
S4 |
90+0 ´ D |
1 |
0 |
0 |
0 |
0 |
1 |
|
|
|
0+1 ´ D |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
|
100 |
100 |
0 |
0 |
0 |
0 |
Dans le tableau optimal, la colonne correspondant à S1 nous donne les coefficients de
D dans la colonne des quantités.|
|
|
|
100 |
200 |
0 |
0 |
0 |
0 |
|
|
|
|
x1 |
x2 |
S1 |
S2 |
S3 |
S4 |
|
100 |
x1 |
40+4/3 D |
1 |
0 |
4/3 |
0 |
-1/3 |
0 |
|
0 |
S2 |
60-14/3 D |
0 |
0 |
-14/3 |
1 |
2/3 |
0 |
|
200 |
x2 |
110-1/3 D |
0 |
1 |
-1/3 |
0 |
1/3 |
0 |
|
0 |
S4 |
50-4/3 D |
0 |
0 |
-4/3 |
0 |
1/3 |
1 |
|
|
|
26000+200 D /3 |
100 |
200 |
200/3 |
0 |
100/3 |
0 |
|
|
|
|
0 |
0 |
-200/3 |
0 |
-100/3 |
0 |
La base reste optimale tant que :
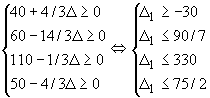 Û - 30 £ D £ 90/7
Û - 30 £ D £ 90/7
Donc tant que 120 £ b1 £ 160,85 la base demeure la même et la solution optimale est stable mais elle change en valeur (exemple: pour D = 3 le vecteur de solutions optimale est (x1,x2,S1,S2,S3,S4)=(44,109,0,46,0,46))
Remarque : D’après le résultat ci-dessus on peut conclure que le coût marginal de 200/3 par hectare de la première ressource n’est valide que si la solution de base demeure stable. Donc si et seulement si 120 £ b1 £ 160,85. Ceci est appelé le domaine de validité du coût marginal.
Exercice 1:
Sans faire de calcul, de combien peut-on modifier la quantité de m3 d’eau sans nuire à la solution optimale ? confirmez votre résultat a l'aide de la méthode d'analyse de sensibilité exposé ci-dessus ?
Exercice 2 :
Déterminer l’intervalle dans lequel peut varier b1 et b3 (les ressources en surface et en main d’œuvre) sans que la base optimale change.
Réponse 2 :

Pour D 1 = 0 (variation nulle de la surface en hectare), la solution optimale est stable pour une variation D 2 des ressources en main d’œuvre entre 570 et 730 heures (-150 £ D 2 £ 90).
Le coût marginal de 100/3 par heure de main d’œuvre de la 3ème ressource n’est valide que dans l’intervalle [570, 730].
c. Analyse de sensibilité sur les coefficients aij
Supposons que dans le problème de l’agriculteur, le nombre d’unités de la ième ressources nécessaire pour produire une unité de produit j, soit (aij +
d ) ou lieu de aij. Ainsi, on se pose la question si la solution optimale demeure stable suite à un tel changement.
i) xj est une variable de base et la ième ressource est totalement utilisée.
Par exemple :
x1 + (4+d )x2 £ 480 Þ x1 + (4 + d )x2 + S3 = 480A l’optimum, la base est inchangée donc
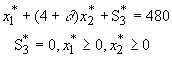
Conclusion: Dans le cas où xj est une variable de base optimale et la ième ressource est totalement utilisée, il est impossible de modifier le coefficient aij sans que la base dans la solution optimale ne change pas (la solution optimale n'est pas satable).
ii) xj est une variable de base et la ième ressource n’est pas totalement utilisée.
Par exemple : (4 +d ) x1 + 2x2 £ 440
Þ (4 + d )x1 +2x2 + S2 = 440
A l’optimum, la solution est inchangée donc
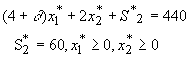
Pour que la base demeure toujours optimale il faut et il suffit que
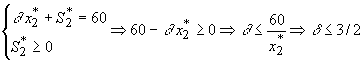
Conclusion: Dans le cas où xj serait une variable de base optimale et où la ième ressource n’est pas totalement utilisée, il est possible de modifier le coefficient aij d’une valeur d ij égale à  et la solution optimale demeure stable.
et la solution optimale demeure stable.
iii) Si xj est une variable hors base (xj = 0). Ceci implique qu’on ne va pas produire le produit j
 Cliquer ici pour enregistrer le chapitre 5 en format Word sur votre disque dur (371 Ko)
Cliquer ici pour enregistrer le chapitre 5 en format Word sur votre disque dur (371 Ko)
![]() Pour tout commentaire envoyer un mail à hatem_masri@yahoo.com
Pour tout commentaire envoyer un mail à hatem_masri@yahoo.com