CHAPITRE 3
On a présenté dans le chapitre précédent une procédure graphique pour résoudre un programme linéaire à deux variables. Par contre, dans la plupart des problèmes réels, on a plus que deux variables à déterminer. Une procédure algébrique pour résoudre les programmes linéaires avec plus que deux variables fera l’objet de ce chapitre. C'est la méthode de simplexe.
Une implémentation de cette procédure à permis de résoudre des programmes avec un peu plus de quelques milliers de variables. Le programme Lindo qu’on présentera dans le chapitre 7 (en version pour étudiant) supporte au plus 200 variables et 100 contraintes.
Dans ce chapitre la méthode de simplexe est présentée pour les problèmes
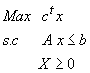
et en utilisant le problème de l’agriculteur :
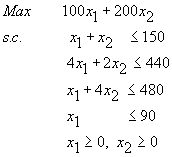
La mise sous forme standard consiste à introduire des variables supplémentaires (une pour chaque contrainte) de manière a réécrire les inégalités (![]() ) sous la forme d'égalités. Chacune de ces variables représente le nombre de ressources non utilisés. On les appelle variable d'écart. La forme standard s'écrit donc :
) sous la forme d'égalités. Chacune de ces variables représente le nombre de ressources non utilisés. On les appelle variable d'écart. La forme standard s'écrit donc :
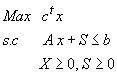 Û
Û 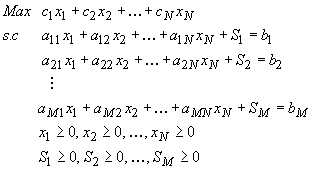
La forme standard du programme linéaire de l'agriculteur est :
Max 100x1 + 200x2 (3.1)
s. c x1 + x2 + S1 = 150 (3.2)
4x1 + 2x2 + S2 = 440 (3.3)
x1 + 4x2 + S3 = 480 (3.4)
x1 + S4 = 90 (3.5)
x1, x2, S1, S2, S3, S4 ³ 0 (3.6)
L'impact de ces variables d'écart sur la fonction objectif est nulle. Ceci explique le fait que leur existence soit tout simplement liée à une mise en forme du programme linéaire initial. Ces variables d'écart peuvent prendre des valeurs nonnegatives. Le fait de donner la valeur des variables d'écart a l'optimum donne une idée du nombre des ressources non utilisées.
III. Revue algébrique de la méthode du simplexe
La question qui se pose : que demande-t-on d’une procédure algébrique ?
En premier lieu, on note que les contraintes du problème (3.2)-(3.5), forment un système de 4 équations et de 6 variables. Or il y a un nombre infini de solutions de ce système d’équations. Donc une procédure algébrique, pour la résolution d’un programme linéaire doit être capable de retrouver les solutions des systèmes d’équations où il y a plus de variables que de contraintes.
En deuxième lieu, ce ne sont pas toutes les solutions qui vérifient (3.2)-(3.5) qui sont des solutions du programme linéaire ; ils doivent en plus satisfaire les contraintes de nonnégativité. Ainsi une procédure algébrique doit être capable d’éliminer, de l’ensemble des solutions qui satisfait (3.2)-(3.1) celles qui n’arrivent pas à satisfaire les contraintes de nonnégativité.
Finalement, une procédure algébrique pour résoudre les programmes linéaires doit être en mesure de choisir parmi les solutions réalisables ceux qui maximisent la fonction objectif.
La méthode de simplexe est une procédure algébrique qui tient compte de ces trois considérations.
Pour illustrer cette procédure, supposons que x2 = 0 et S1 = 0. Notre système devient
x1 = 150 x1 = 150
x1 + S2 = 440 S2 = 340
4x1 + S3 = 480 S3 = -120
x1 + S4 = 90 S4 = -60
Les variables x1, S2, S3 et S4 (non nulles) sont dites variables de base et les variables S1, x2, (nulles) sont dites variables hors base.
Généralement, si on a un programme linéaire standard constitué de n variables et m contraintes
(n
On note qu’une solution de base n’est pas toujours réalisable. C’est le cas de la solution qu’on vient de retrouver.
Une solution réalisable de base serait celle où x1 = x2 = 0, ainsi on a :
S1 = 150
S2= 440
S3 = 480
S4 = 90
Cette solution correspond à un point extrême de l’ensemble des solutions réalisables qui est l’origine O.
Pour la méthode de simplexe une solution réalisable de base initiale est demandée. Une telle solution peut être retrouvée en annulant toutes les variables de décision. Ce qui correspond dans notre exemple au point d’origine O.
A partir de ce point la méthode de simplexe va générer successivement des solutions réalisables de base pour notre système d’équations en s’assurant que la valeur de la fonction objectif est en train d’augmenter jusqu'à localiser la solution optimale du problème qui est un point extrême de l’espace des solutions réalisables donc une solution réalisable de base.
Ainsi, on peut décrire la méthode de simplexe comme étant une procédure itérative qui passe d’une solution réalisable de base à une autre jusqu’à atteindre la solution optimale.
La description mathématique de ce processus fera l’objet de la section suivante.
 Cliquer ici pour enregistrer le chapitre 3 en format Word sur votre disque dur (151 Ko)
Cliquer ici pour enregistrer le chapitre 3 en format Word sur votre disque dur (151 Ko)
![]() Pour tout commentaire envoyer un mail à hatem_masri@yahoo.com
Pour tout commentaire envoyer un mail à hatem_masri@yahoo.com