V. Recherche de la solution optimale
Si nous retraçons l’ensemble des droites parallèles relatives à différentes valeurs de la fonction objectif sur la figure qui représente l’ensemble des solutions réalisables, on peut localiser la solution optimale. Elle correspond à la solution réalisable qui intercepte la droite à la plus petite valeur de z.
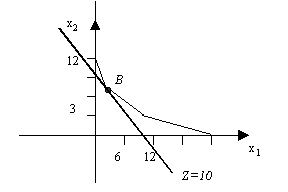
Dans notre exemple, la solution optimale est l’intersection des deux contraintes ![]() et
et ![]() . Une évaluation des coordonnées de ce point revient à résoudre le système linéaire suivant :
. Une évaluation des coordonnées de ce point revient à résoudre le système linéaire suivant :
![]()
Elle correspond d’après le graphique au point (2,8). Donc la prescription optimale est de 2 pilules de petite taille et 8 pilules de grande taille. Le nombre de pilules (la valeur de la fonction objectif) est égale à 10.
b. Résolution par énumération :
On remarque que la solution optimale du problème de médecine est un point extrême qui se trouve sur le bord de l’ensemble des solutions. Une telle solution est dite solution réalisable de base.
On peut admettre le résultat suivant : " Si un programme linéaire admet une solution optimale alors il existe une solution réalisable de base pour laquelle la fonction objectif atteint la valeur optimale "
Une méthode de résolution du programme linéaire consiste donc à déterminer les solutions réalisables de base (les points d’intersection des droites qui forment les contraintes) et à calculer pour chaque point la valeur de la fonction objectif. La solution du programme linéaire est la solution à qui on associe la valeur optimale de la fonction objectif.
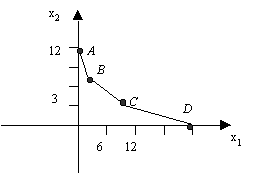
Dans le problème de médecine, l’ensemble des solutions réalisables de base présente 4 points extrêmes A(0,12), B(2,8), C(23/11,126/11) et D(24,0). La valeur de la fonction objectif associée respectivement à A, B, C et D est 12, 10, 149/11 et 24. On vérifie bien que B est la solution optimale du problème avec une valeur optimale égale à 10.
![]() Cliquer ici pour enregistrer le chapitre 2 en format Word sur votre disque dur (452 Ko)
Cliquer ici pour enregistrer le chapitre 2 en format Word sur votre disque dur (452 Ko)
![]() Pour tout commentaire envoyer un mail à hatem_masri@yahoo.com
Pour tout commentaire envoyer un mail à hatem_masri@yahoo.com