V. Exemples de formulations
Limité au départ aux problèmes industriels et militaires, de nos jours plusieurs problèmes de divers domaines sont représentés ou approximés par des modèles de PL. L’utilisation de ces techniques de modélisation s’est renforcée encore après avoir construit des algorithmes et des logiciels capables de résoudre de plus larges problèmes avec autant de variables de décision que de contraintes.
La tâche de formulation demande généralement une certaine expertise et connaissance du problème pour pouvoir relever facilement les différentes composantes du problème et ainsi donner un programme qui modélise au mieux la situation réelle. Dans ce qui suit, on présentera quelques exemples de formulation en programme linéaire liés à différents problèmes de décision :
Exemple 1 : Problème d’agriculture
Un agriculteur veut allouer 150 hectares de surface irrigable entre culture de tomates et celles de piments. Il dispose de 480 heures de main d’œuvre et de 440 m3 d’eau. Un hectare de tomates demande 1 heure de main d’œuvre, 4 m3 d’eau et donne un bénéfice net de 100 dinars. Un hectare de piments demande 4 heures de main d’œuvre, 2 m3 d’eau et donne un bénéfice net de 200 dinars.
Le bureau du périmètre irrigué veut protéger le prix des tomates et ne lui permet pas de cultiver plus de 90 hectares de tomates. Quelle est la meilleure allocation de ses ressources ?
Formulation du problème en un PL :
Etape 1 : Identification des variables de décision. Les deux activités que l’agriculteur doit déterminer sont les surfaces à allouer pour la culture de tomates et de piments :
On vérifie bien que les variables de décision x1 et x2 sont positives : ![]() .
.
Etape 2 : Identification des contraintes. Dans ce problème les contraintes représentent la disponibilité des facteurs de production :
Etape 3 : Identification de la fonction objectif. La fonction objectif consiste à maximiser le profit apporté par la culture de tomates et de piments. Les contributions respectives 100 et 200, des deux variables de décision x1 et x2 sont proportionnelles à leur valeur. La fonction objectif est donc ![]()
Le programme linéaire qui modélise le problème d’agriculture est :
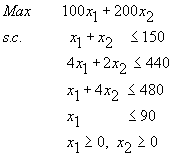
Cliquer ici pour enregistrer le chapitre 1 en format Word sur votre disque dur (172 Ko)
![]() Pour tout commentaire envoyer un mail à hatem_masri@yahoo.com
Pour tout commentaire envoyer un mail à hatem_masri@yahoo.com