II. Exemple prototype. Le problème du voyageur
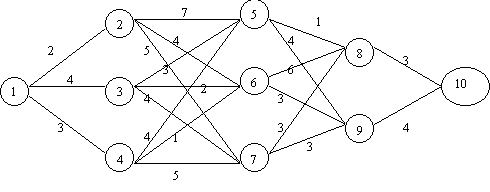
Un postier décide d’effectuer un voyage entre différentes villes qu’il ne connaît pas. Son but est de choisir le chemin le moins dangereux. Pour choisir son chemin, il s’informe auprès des assurances sur les différentes valeurs des polices d’assurance de vie entre les différentes routes possibles du voyage.
Le trajet du postier est composé de 4 étapes (voir figure) et il doit arriver à la ville numérotée 10 en partant de la ville numérotée 1. Les autres numéros représentent les villes susceptibles d’être traversées. Les arcs entre ces nœuds représentent les différents trajets possibles et les valeurs cij au-dessus des arcs représentent le prix de la police d’assurance vie relatif au trajet décrit par l’arc.
Le chemin le moins dangereux est celui qui admet la plus petite valeur de la police d’assurance vie
Exemple : Si le voyageur empreinte le trajet 1
® 2® 6® 9® 10 , le coût total de la police d’assurance est 13Soit xn (n=1, ..., 4) les variables de décisions relatives à chacune des 4 étapes. Le chemin à suivre par le voyageur est 1
® x1® x2® x3® x4 avec x4 = 10.Soit fn (S, xn) le coût total de la police d’assurance vie pour le reste des étapes sachant que nous somme à l’état S de l’étape n et que la destination choisie est xn.
Etant donné S et n, soit ![]() la valeur de xn qui minimise fn (S, xn) et soit
la valeur de xn qui minimise fn (S, xn) et soit ![]() (S) la valeur minimale de fn (S, xn). (
(S) la valeur minimale de fn (S, xn). (![]() (S)= fn (S,
(S)= fn (S, ![]() )).
)).
L’approche de la programmation dynamique repose sur l’idée qu’un chemin ne peut être optimal que si chacune des ses composantes est elle même optimale. La démarche de la programmation dynamique consiste à étudier d’abord les sous problèmes qui se situent chronologiquement les derniers et sur un principe de retour en arrière.
L’objectif est donc de trouver la valeur de ![]() (1). Pour l’avoir, la programmation dynamique va essayer d’évaluer avec une procédure de chaînage en arrière
(1). Pour l’avoir, la programmation dynamique va essayer d’évaluer avec une procédure de chaînage en arrière ![]() (s),
(s), ![]() (s),
(s), ![]() (s) et enfin
(s) et enfin ![]() (1).
(1).
A chaque étape, on va essayer d’évaluer pour chaque état s, la valeur de f (S, xn) pour chaque destination xn possible, puis de retrouver la meilleure destination ![]() (celle qui correspond au plus petit coût f(S, xn)) et aussi la valeur de
(celle qui correspond au plus petit coût f(S, xn)) et aussi la valeur de ![]() (s).
(s).
Etape 4
|
x4 S |
f4(S, x4)) |
|
|
|
8 |
3 |
3 |
10 |
|
9 |
4 |
4 |
10 |
Etape 3
|
|
f3(S, x3)=Csx3+ |
|
||
|
x3 S |
8 |
9 |
|
|
|
5 |
4(=1+3) |
8(=4+4) |
4 |
8 |
|
6 |
9 |
7 |
7 |
9 |
|
7 |
6 |
7 |
6 |
8 |
Etape 2
|
|
f2(S, x2)=Csx2+ |
|
||||
|
x2 S |
5 |
6 |
7 |
|
|
|
|
2 |
11 |
11 |
12 |
11 |
5 ou 6 |
|
|
3 |
7 |
9 |
10 |
7 |
5 |
|
|
4 |
8 |
8 |
11 |
8 |
5 ou 6 |
|
Etape 1
|
|
f1(S, x1)=Csx1+ |
|
||||
|
x1 S |
2 |
3 |
4 |
|
|
|
|
1 |
13 |
11 |
112 |
11 |
3 ou 4 |
|
La valeur de ![]() (1) = 11 représente le coût total minimal de la police d’assurance vie. Le chemin optimal n’est unique puisque dès le départ on peut choisir
(1) = 11 représente le coût total minimal de la police d’assurance vie. Le chemin optimal n’est unique puisque dès le départ on peut choisir ![]() = 3 ou 4, donc l’ensemble de ces chemins est:
= 3 ou 4, donc l’ensemble de ces chemins est:
1
® 3 ® 5 ® 8 ® 101
® 4 ® 5 ® 8 ® 101
® 4 ® 6 ® 9 ® 10Exercice 1 : (Problèmes de transport)
Modéliser le problème de plus court chemin en utilisant la programmation linéaire ?
(Aide: Utiliser des variables du type binaires xi=0 ou 1)
 Cliquer ici pour enregistrer le chapitre 7 en format Word sur votre disque dur (436 Ko)
Cliquer ici pour enregistrer le chapitre 7 en format Word sur votre disque dur (436 Ko)
![]() Pour tout commentaire envoyer un mail à hatem_masri@yahoo.com
Pour tout commentaire envoyer un mail à hatem_masri@yahoo.com