INDEX

1. Solve : Résoudre le modèle dont la fenêtre est active
2. Compile Model : Compiler (sans résoudre) le modèle dont la fenêtre est active
3. Debug : Débugger le modèle dont la fenêtre est active, s’il est non réalisable ou non borné. Dans le cas d’un problème non réalisable, la commande Debug détecte l’ensemble des contraintes (sufficient set), dont l’élimination est suffisante pour garantir une solution optimale. Et il détermine aussi un ensemble de contraintes (necessary set), dont la modification entraîne nécessairement un modèle réalisable. Dans le cas d’un problème non borné, la commande Debug détecte l’ensemble des variables de décision (sufficient set), dont la fixation de leurs valeurs est suffisante pour garantir une solution optimale. Et il détermine aussi un ensemble de variables de décision (necessary set), dont la modification entraîne nécessairement un modèle borné.
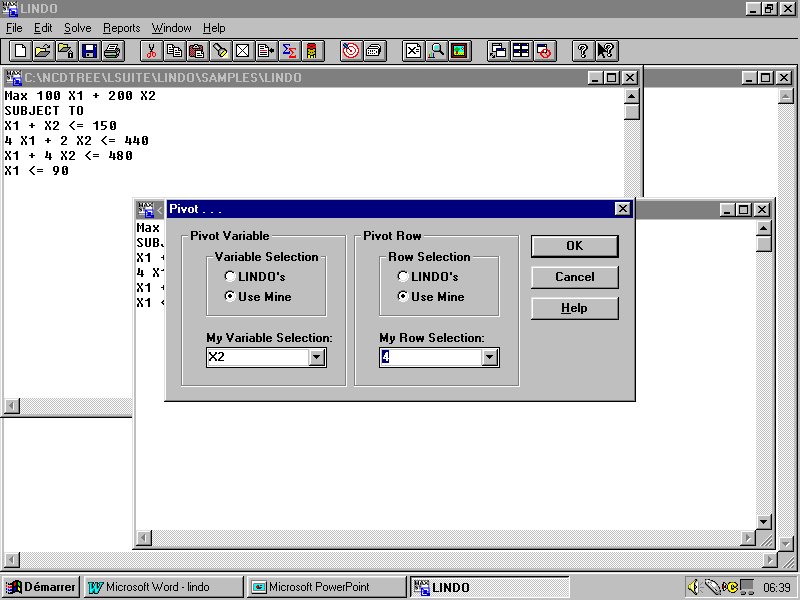
4. Pivot : Une des opérations fondamentales dans la méthode de Simplexe est l’opération pivot, qui correspond à une itération du simplexe. Lindo nous donne la possibilité de choisir nous même les variables entrantes et sortantes et nous permet ainsi de résoudre le programme itération par itération.

Exemple : Essayons de résoudre le problème de l’agriculteur en utilisant la commande " Pivot ".

La variable entrante dans le premier tableau de Simplexe est X2 et la variable sortante est la variable d’écart de la contrainte dans la 4^ième ligne.



Le rapport suivant s’affiche :



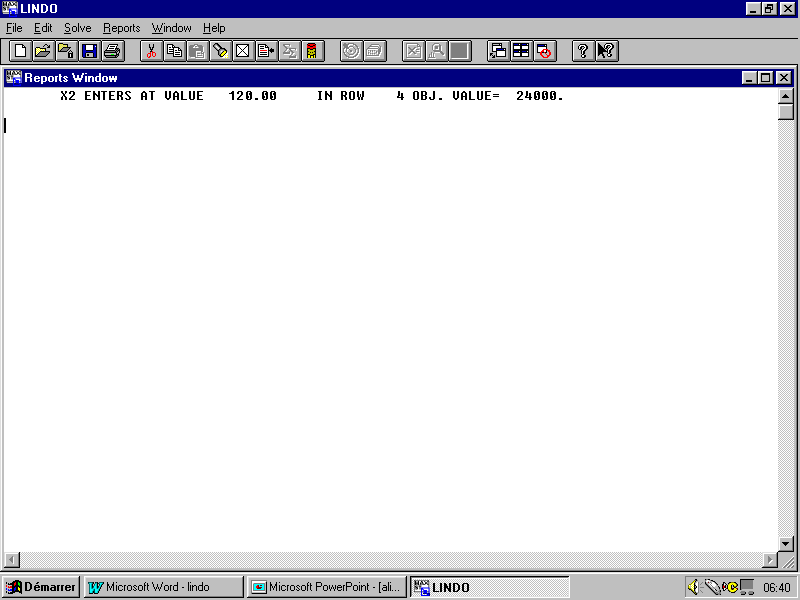
Donc cette itération a fait passer la valeur de la fonction objectif à 24000.

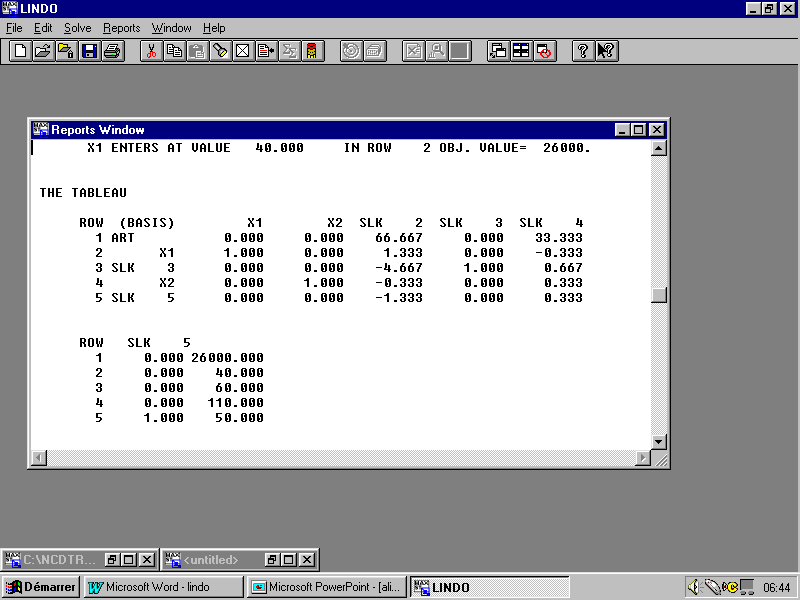
Pour pouvoir choisir les variables entrantes et sortantes on peut afficher le tableau de Simplexe relatif à la dernière itération en utilisant la commande " Tableau " dans le menu " Reports ". On obtient :



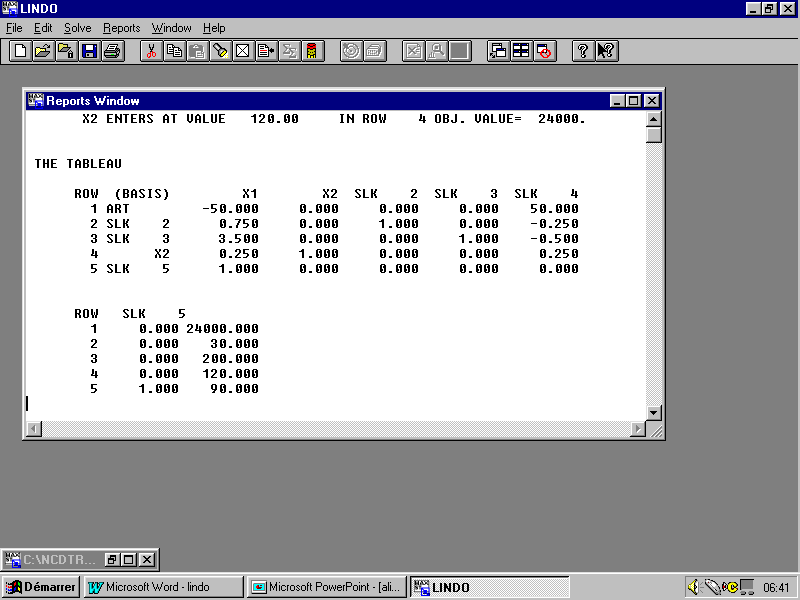
D’après le tableau ci-dessus, la variable entrante est X1 et la variable sortante est SLK 2.

On obtient ainsi le résultat suivant :



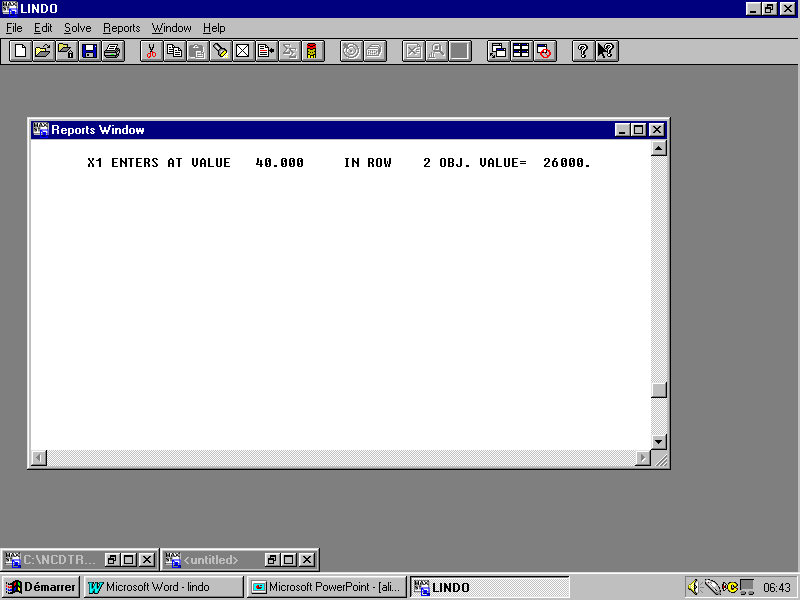
La valeur de la fonction objectif est optimale et on peut vérifier que le tableau de simplexe relatif à cette dernière itération est optimal :



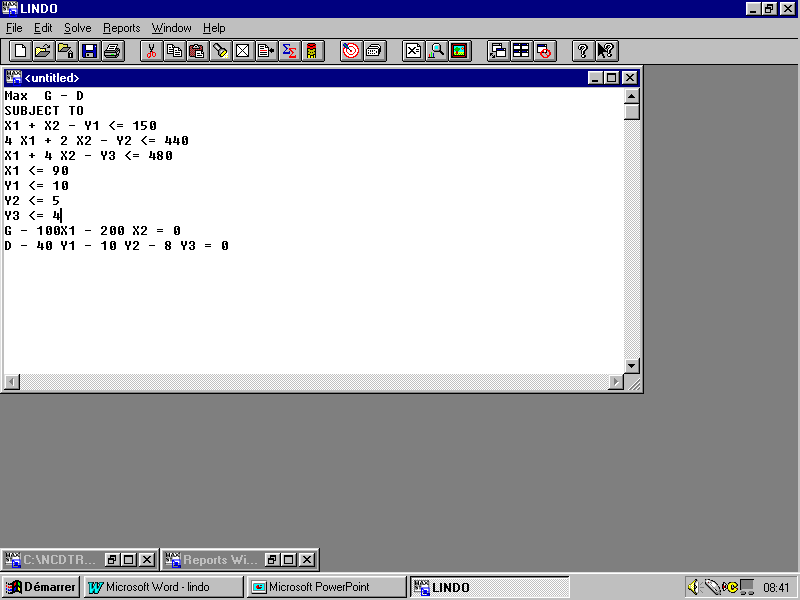
5. Preemptive Goal : Cette commande peut résoudre un problème à objectif multiples en adoptant une manière lexicographique. Ainsi on optimise le premier objectif puis le second sous une contrainte supplémentaire que le premier est égale à la valeur optimale déjà trouvée. Plus précisément, supposons que l’agriculteur peut acheter des ressources supplémentaires avec un prix de 40 dinars pour un hectare de terrain(Y1), 10 dinars le m³ d’eau (Y2) et 8 dinars l’heure supplémentaire de main d’œuvre (Y3). Les quantités disponibles sur le marché respectivement pour Y1, Y2 et Y3 sont de 10 hectares de terrain, 5 m³ d’eau et 4 heures de main d’œuvre. On appelle G le gain issu de la culture et D les dépenses d’achat des ressources supplémentaires. Le programme peut s’écrire sous cette forme :

Cliquer ici pour enregistrer le chapitre 6 en format Word compressé (.zip) sur votre disque dur (909 Ko)

Pour tout commentaire envoyer un mail à hatem_masri@yahoo.com