II. Résolution d’un exemple
Dans cette section, et sur la base de l’exemple de l’agriculteur, on va focaliser notre attention sur les opérations suivantes : introduire les données, résoudre le problème, et analyser les résultats que donne LINDO.
a. Le problème de l’agriculteur
Le programme linéaire qui modélise le problème de l’agriculture est :
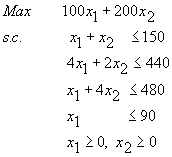
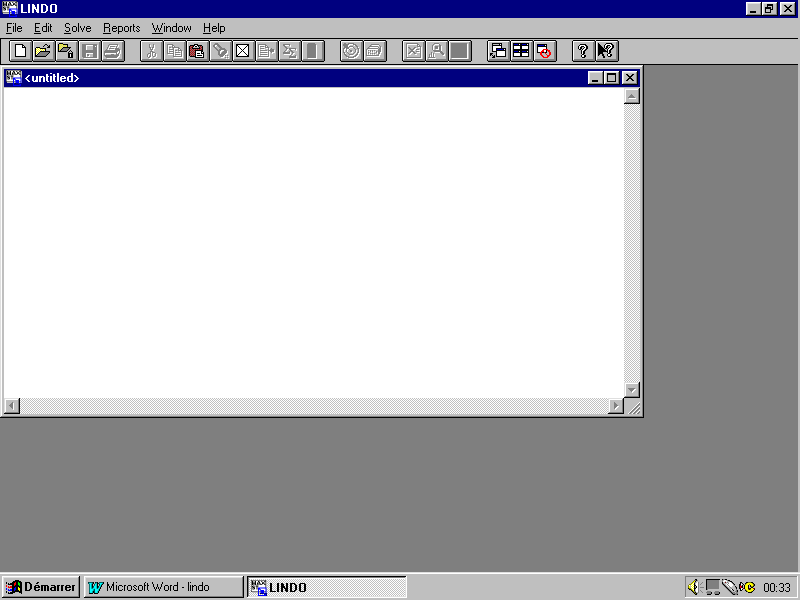
Double cliquer sur l’icône "lindo 6.0 for Windows " de votre menu démarrer/programmes. Le logiciel va s’exécuter et vous aurez cette fenêtre qui s’affiche sur votre écran :
Dans tous les modèles de Lindo la fonction objectif est définie en première ligne. Dans notre exemple la fonction objectif est :
![]()
Les tirés bas indique la présence d’un espace obligatoire entre les entrées pour pouvoir les différentiées.
Il faut noter qu’on peut remplacer x1 et x2 par n’importe quel mot qui indique ces deux variables, par exemple, on peut remplacer x1 par "tomates" et x2 par "piments". Une autre caractéristique est que Lindo ne fait pas de différence entre majuscule et minuscule. Pour lui la variable " TOMATE " est la même que la variable " tomAtE ".
Pour commencer à écrire les contraintes, il faut introduire la mention " subject to " ou tout simplement son abréviation " st ".
Dans notre exemple les contraintes sont :
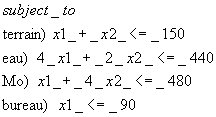
On remarque qu’on peut appeler chaque contrainte par un nom nominatif que Lindo va utiliser pour afficher les résultats.
L’écran qu’on obtient après avoir introduit les différents paramètres est le suivant :
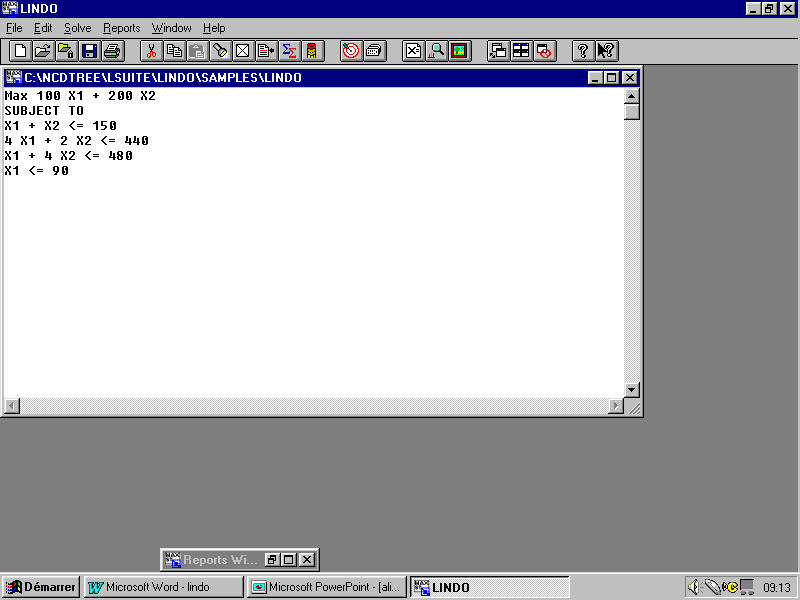
On n’a pas à ajouter les contraintes de non-négativité, Lindo suppose par défaut que les variables de décision sont de types nonnégative.
Après avoir écrit convenablement le programme linéaire, on passe maintenant à la résolution.
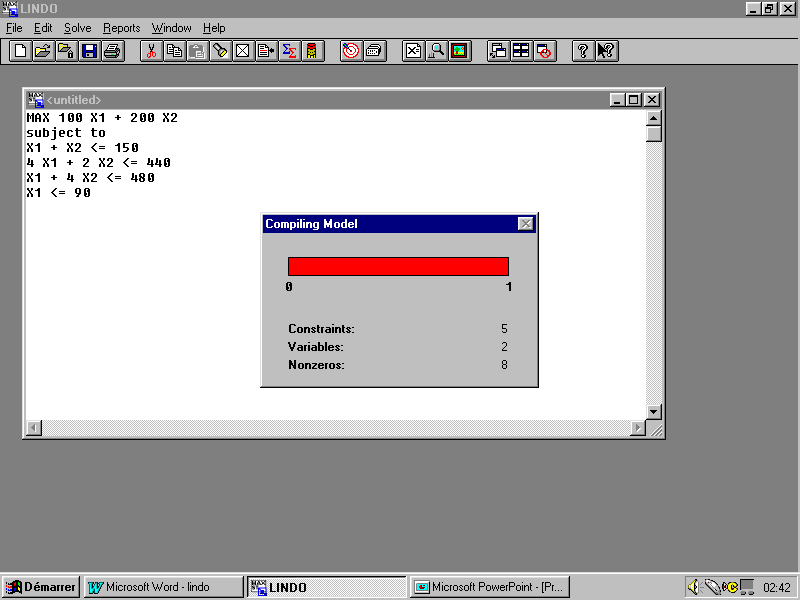
Pour résoudre notre programme il faut cliquer sur le bouton " 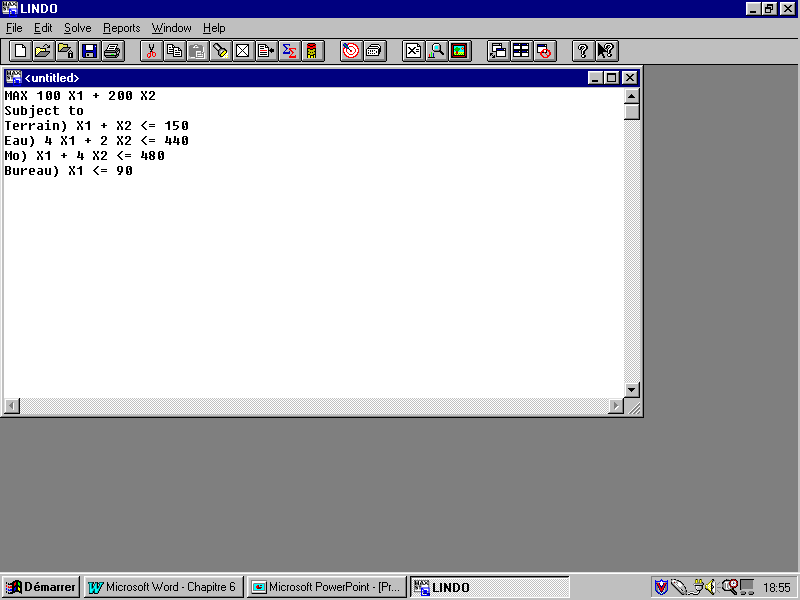
Lors de la compilation, on voit une barre qui montre le pourcentage de travail effectué.
d. Interprétation des résultats
S’il n’y a pas d’erreur de formulation, Lindo va commencer à résoudre le problème. Par défaut, il va vous demander si vous voulez faire une analyse de sensibilité. Pour le moment on va répondre " Non ".
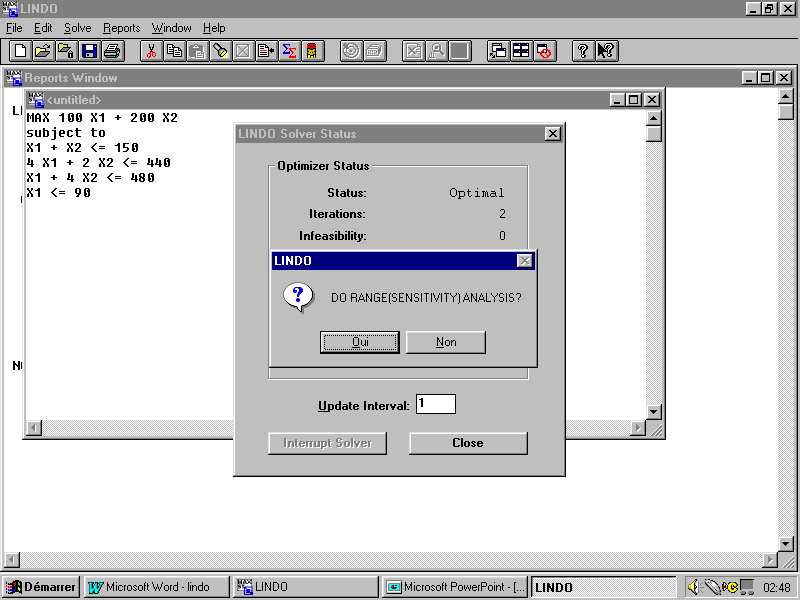
Avant que Lindo nous propose un premier rapport sur la solution optimale, il nous donne l’état du problème exprimé par cette fenêtre :
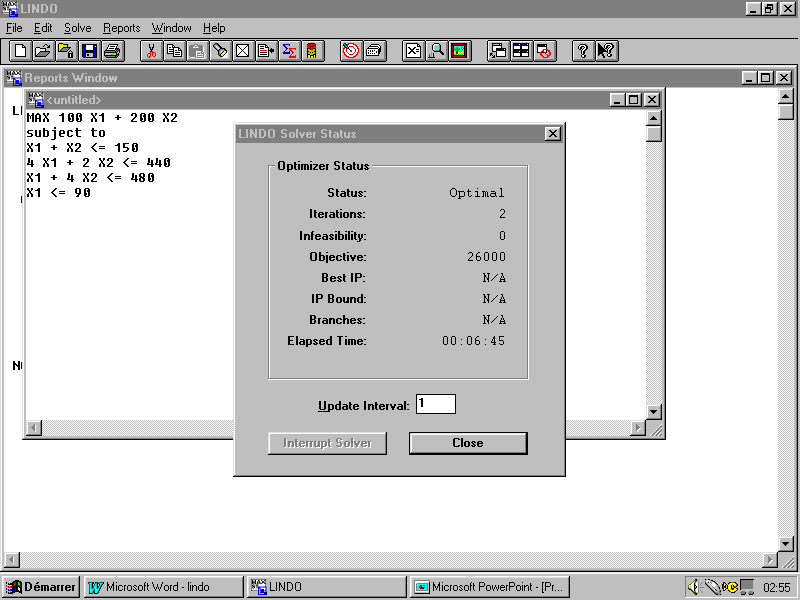
Ce rapport préliminaire nous indique que :
Si on ferme cette fenêtre, on remarque qu’un autre rapport s’affiche. Ce rapport contient des informations sur la solution optimale.
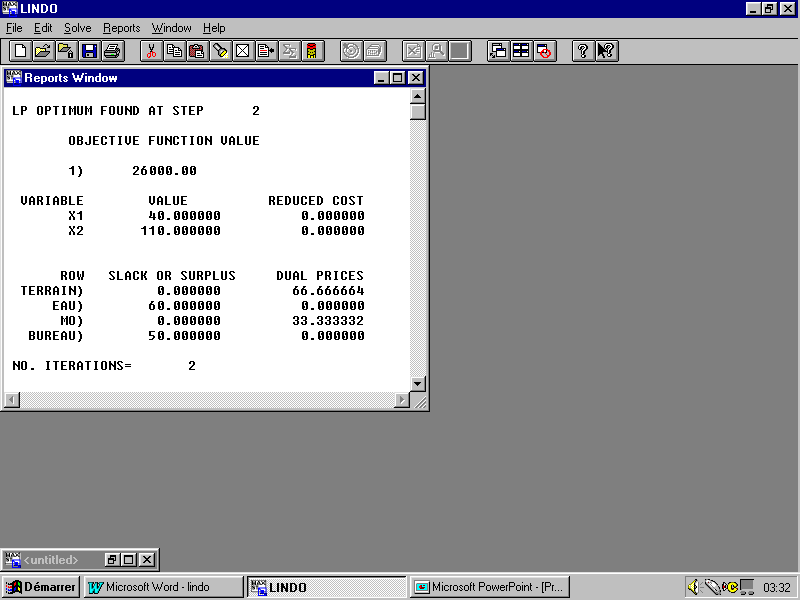
Dans le tableau ci-dessus s’affichent dans la première colonne les différentes variables de décision et aussi les variables d’écart relatives à chaque contrainte du programme. Leurs valeurs sont données dans la deuxième colonne. On vérifie bien que la solution optimale coïncide avec la solution déjà retrouvée dans les précédants chapitres. La troisième colonne représente les valeurs nettes, i.e.![]() . Pour les variable d’ecart c’est les prix duals.
. Pour les variable d’ecart c’est les prix duals.
 Cliquer ici pour enregistrer le chapitre 6 en format Word compressé (.zip) sur votre disque dur (909 Ko)
Cliquer ici pour enregistrer le chapitre 6 en format Word compressé (.zip) sur votre disque dur (909 Ko)
![]() Pour tout commentaire envoyer un mail à hatem_masri@yahoo.com
Pour tout commentaire envoyer un mail à hatem_masri@yahoo.com