Dualité et analyse de sensibilité

Dans ce chapitre, on va étudier des notions relatives au programmes linéaires tels que le programme dual, les coûts marginaux ainsi que des techniques de validation de la solution d’un programme linéaire, c’est à dire l’analyse de sensibilité.

Nous allons commencer ce chapitre par donner quelques termes clés du jargon utilisé pour interpréter économiquement les différents résultats du programme linéaire.

Les éléments clés d’un programme linéaire standard sont :

- La fonction objectif dite fonction économique. Cette fonction peut représenter un coût, un profit, etc...

- Les contraintes sont composées, des coefficients a_ij de la matrice A, dite matrice technologique, et des constantes b_i, qui forment le vecteur du second membre. Le second membre peut représenter la disponibilité des ressources, les niveaux de demande etc...

- Les variables d’écart peuvent représenter, par exemple dans le problème de l’agriculteur, l’excédent de chacune des ressources : terrain, eau, heures de travail, bureau d’irrigation. Elles sont aussi dites variables de surplus.

Quand une variable d’écart est nulle, on dit que la contrainte correspondante est saturée. Dans le problème de l’agriculteur les contraintes terrain et main d’œuvre sont saturées. Elles sont dites aussi restrictives car une variation du second membre (par exemple) engendre un changement dans la valeurs de la solution optimale.

Toute contrainte non saturée à l’optimum n’est pas restrictive pour le problème, c’est à dire qu’elle n’a aucune influence sur la solution considérée.

Définition: Coût marginal

Par définition, on appelle coût marginal d’un bien l’augmentation minimale de dépenses, par rapport à la solution optimale, qui résulterait de l’utilisation d’une unité supplémentaire de ce bien, lorsque le problème posé consiste à produire des biens au moindre coût.

Si le problème posé consiste à transformer des biens pour vendre une production avec un meilleur profit et l’augmentation maximale de revenu qui résulte de la possibilité de disposer d’une unité supplémentaire de l’un des biens, est la valeur marginale de ce bien. Très souvent, on emploie également dans ce cas le qualificatif coût marginal.

Remarque : Les coûts marginaux sont donc les effets nets associés aux variables d’écart, puisque ce sont ces variables qui déterminent les excédents (ou les insuffisances) de biens.

Si une variable d’écart n’est pas nulle, dans la solution optimale, c’est que le bien correspondant est déjà excédentaire. Par conséquent, le fait de disposer d’une unité supplémentaire de ce bien n’aura aucune influence sur le revenu. On dit alors que ce bien à une valeur marginale nulle, ou par extension, que la variable d’écart associée à ce bien a une valeur marginale nulle.

Par contre, si une variable d’écart est nulle dans la solution optimale, c’est que le bien correspondant est totalement utilisé. Par la suite une variation de la disponibilité aura généralement une influence sur le revenu. C’est pourquoi cette variable d’écart nulle dans la solution optimale à une valeur marginale non nulle, et cette valeur marginale précise la variation de la fonction économique résultant de l’utilisation d’une unité supplémentaire du bien associé.

Exemple : Dans le problème de l’agriculteur on a

• Le coût marginal lié à est

• Le coût marginal lié à est 0 et à l'optimum =0

Le système de contraintes dans le programme linéaire relatif au tableau de simplexe optimal du problème de l’agriculteur est

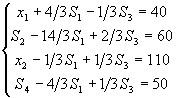
La fonction économique s’écrit

Si on exprime en fonction de et (variables hors base) en utilisant le système d’équation ci dessus on a

La valeur 26000 correspond à la valeur optimale de la fonction économique.

Si alors un hectare de terrain de moins à utiliser, donc une réduction de dinars de la valeur de la fonction objectif.

Si on ajoute 3 hectares de terrains , avec l’hypothèse que les autres quantités restent inchangées alors le revenu augmente de

On vérifie ceci, si on résout le programme linéaire

,

On trouve que la valeur optimale va augmenter de 200 dinars est devient 26 200 dinars.

Exercice : Expliquer graphiquement que si on ajoute des d’eau, on aura aucune amplification dans la fonction objectif.

Remarque : Dans le cas où on diminuerait d’eau, la solution optimal devient dégénérée.

Les valeurs marginales apportent donc des renseignements économiques particulièrement intéressantes, mais il faut les utiliser avec prudence car leur domaine de validité est limité.

Par exemple, si on ajoute 30 hectares de terrains aux 150 déjà disponibles dans le problème de l’agriculteur, le revenu augmentera de . Ceci n’est pas vrai, parce que si on résout le programme linéaire suivant :

,

La valeur optimale du programme linéaire ci-dessus est de 26 875,14 donc le revenu n’a pas augmenté de 2000 dinars comme prévu.